Résumé

Avant la formation du monde, tous les éléments étaient secoués au hasard, mais occupaient déjà des places différentes.

Dieu commença par leur donner une configuration distincte au moyen des idées et des nombres.

D’abord il est évident que le feu, la terre, l’eau et l’air sont des corps.

Or les corps ont pour éléments des triangles d’une infinie petitesse.

Ces triangles sont scalènes = 3 côtés inégaux,
et sans symétrie .

ou isocèles. = 2 côté égaux

Les scalènes (3 côtés inégaux) engendrent en se combinant trois solides :
la pyramide,
l’octaèdre,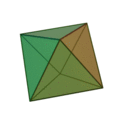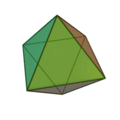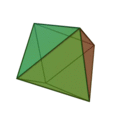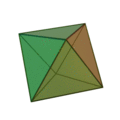
l’icosaèdre ;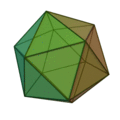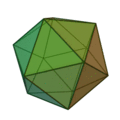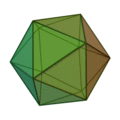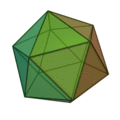

Et ... le quatrième solide :
les isocèles (2 côtés égaux) un seul : le cube. 12x3, la terre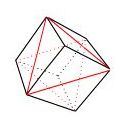

De ces solides dérivent les quatre corps élémentaires :

[le cercle est le germe de la terre, terre représentée par un cube
(étude des ronds , Noeudrondlogie)]

la pyramide celui du feu, 4x3,
l’octaèdre celui de l’air, 8x3,
et l’icosaèdre celui de l’eau. 20x3,

le Dodécaèdre représente le Tout, 12x5 (12 pentagones),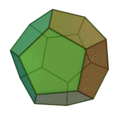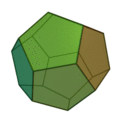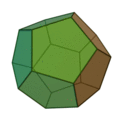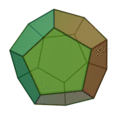

La terre ( le cube) ne peut pas se transformer en une autre espèce,

mais les trois autres éléments le peuvent.

Comment se fait-il que les éléments ne cessent pas de se mouvoir et de se traverser les uns les autres ?

proposition


C’est que le circuit de l’univers, comprenant en lui les diverses espèces, est circulaire et tend naturellement à revenir sur lui-même. Aussi comprime-t-il tous les corps et il ne permet pas qu’il reste aucun espace vide, et cette compression pousse les petits corps dans les intervalles des plus grands et fait que les plus grands forcent les petits à se combiner, et ainsi tous se déplacent pour gagner la place qui leur convient.

Diverses espèces de corps

Il y a diverses espèces de feu, d’air et d’eau.
L’or, le cuivre, le vert-de-gris sont des variétés d’eau ;
la grêle, la glace, la neige en sont d’autres, les sucs aussi ; le vin, l’huile, le miel, le verjus sont formés de feu et d’eau.
La terre comprimée par l’air forme la pierre, la soude et le sel.

Les 4 éléments, la géométrie, la topologie

D’abord il est évident pour tout le monde que
le feu, la terre, l’eau et l’air sont des corps.
Or, le genre corporel a toujours de la profondeur, et la profondeur p117
est, de toute nécessité, enclose par la nature de la surface,
et toute surface de formation rectiligne est composée de triangles

Or, tous les triangles dérivent de deux triangles,
dont chacun a un angle droit et les deux autres aigus.

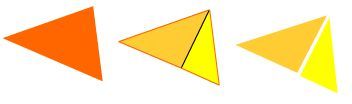
L’un de ces triangles a de chaque côté une partie de l’angle droit divisée par de côtés égaux ;

l’autre, des parties inégales
d’un angle droit divisées par des côtés inégaux.

L'origine du feu... et des corps

Telle est l’origine que nous assignons au feu

(un Feu pyramides)

et aux autres corps, suivant la méthode qui combine la vraisemblance avec la nécessité.

Quant aux origines plus lointaines encore, elles ne sont connues que de Dieu et des hommes qu’il favorise.

Maintenant, il faut expliquer comment peuvent se former les plus beaux corps, qui sont au nombre de quatre, et dissemblables entre eux, mais tels que certains d’entre eux peuvent être engendrés les uns des autres en se dissolvant.

Si nous y réussissons, nous tiendrons la vérité sur l’origine de la terre et du feu et des corps qui leur servent de termes moyens.

La beauté des corps géométriques

Car nous n’accorderons à personne qu’on puisse voir des corps plus beaux que ceux-là, chacun d’eux formant un genre unique.

Appliquons-nous donc à constituer harmoniquement ces quatre espèces de corps supérieurs en beauté, afin de pouvoir dire que nous en avons bien compris la nature.

Or, de nos deux triangles, p118
celui qui est isocèle (2 côtés égaux) n’admet qu’une forme ;

celui qui est scalène (3 côtés inégaux) un nombre infini (de formes)
.

Dans ce nombre infini, il nous faut encore choisir le plus beau, si nous voulons commencer correctement.

Maintenant, si quelqu’un peut en choisir et en indiquer un plus beau pour en former ces corps, je lui cède le prix et le tiens non pour un ennemi, mais pour un ami.

Pour nous, parmi ces nombreux triangles, il en est un que nous regardons comme le plus beau à l’exclusion des autres :
c’est celui dont est formé le troisième triangle (isocèle droit) ,
le triangle équilatéral.

Pourquoi ? Ce serait trop long à dire.
Mais si quelqu’un, soumettant le cas à sa critique, en découvre la raison, je lui accorderai volontiers le prix.

Choisissons donc deux triangles
dont le corps du feu et celui des autres corps ont été constitués,
l’un isocèle, l’autre dans lequel le carré du grand côté est triple du carré du petit.

Ce que nous avons dit là-dessus était obscur : c’est le moment de préciser davantage.

Les quatre espèces de corps nous paraissaient toutes naître les unes des autres : c’était une apparence trompeuse.

La métamorphose triangulaire, trianglo-génèse

En effet,
les triangles que nous avons choisis donnent naissance à quatre types, et, tandis que
- trois sont construits d’un même triangle, celui qui a les côtés inégaux (scalène),

1) scalène, 2) isocèle droit 3) scalène droit,
- le quatrième seul ( équilatéral) a été formé du triangle isocèle (droit).
                     
isocèle droit,           permet               l'équilatéral

Il n’est, par suite, pas possible qu’en se dissolvant, ils naissent tous les uns des autres, par la réunion de plusieurs petits triangles en un petit nombre de grands et réciproquement ; p119
ce n’est possible que pour les trois premiers.

Comme ils sont tous trois formés d’un même triangle,
quand les plus grands corps se désagrègent,
un grand nombre de petits peuvent se former des mêmes triangles,
en prenant la figure qui leur convient ;

et inversement, quand beaucoup de petits corps se désagrègent en leurs triangles,
leur nombre total peut former une autre espèce de corps d’un seul volume et de grande taille.
Voilà ce que j’avais à dire sur leur génération mutuelle.

La première chose à expliquer ensuite, c’est la forme que chacun d’eux a reçue et la combinaison de nombres dont elle est issue.

Naissance du triangle équilatéral

Je commencerai par la première espèce, qui est composée des éléments les plus petits.
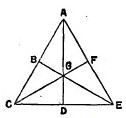
Elle a pour élément le triangle dont l’hypoténuse est deux fois plus longue que le plus petit côté.

                    
Si l’on accouple une paire de ces triangles par la diagonale et qu’on fasse trois fois cette opération, de manière que les diagonales et les petits côtés coïncident en un même point comme centre, ces triangles, qui sont au nombre de six, donnent naissance à un seul triangle, qui est équilatéral.

Génèse des solides

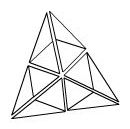
Quatre de ces triangles équilatéraux réunis selon trois angles plans forment un seul angle solide, qui vient immédiatement après le plus obtus des angles plans. Si l’on compose quatre angles solides,
on a la première forme de solide, qui a la propriété de diviser la sphère dans laquelle il est inscrit en parties égales et semblables. p120
Le tétraèdre, le Feu, 4x3
     

La seconde espèce est composée des mêmes triangles.
Quand ils ont été combinés pour former huit triangles équilatéraux, ils composent un angle solide unique, fait de quatre angles plans.
Quand on a construit six de ces angles solides,
le deuxième corps se trouve achevé. L'Octaèdre, l'Air, 8x3

Le troisième est formé de la combinaison de
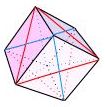
deux fois soixante triangles élémentaires, c’est-à-dire de douze angles solides, dont chacun est enclos par cinq triangles plans équilatéraux,
l'Icosaèdre, l'eau, 20x3,

et il y a vingt faces qui sont des triangles équilatéraux. p121

Triangle isocèle et 4 eme corps

Après avoir engendré ces solides, l’un des triangles élémentaires a été déchargé de sa fonction,
et c’est le triangle isocèle qui a engendré la nature du quatrième corps. La terre.

Groupés par quatre, avec leurs angles droits se rencontrant au centre, ces isocèles ont formé un quadrangle unique équilatéral.

Six de ces quadrangles, en s’accolant, ont donné naissance à huit angles solides, composés chacun de trois angles plans droits,
        
et la figure obtenue par cet assemblage est le cube, qui a pour faces six tétragones de côtés égaux.

La 5 eme combinaison

Il restait encore une cinquième combinaison.

Le Dodécaèdre, le Tout, 12x5,
Dieu s’en est servi pour achever le dessin de l’univers.
En réfléchissant à tout cela, on pourrait justement se demander s’il faut affirmer qu’il y a des mondes en nombre infini ou en nombre limité.

Or croire qu’ils sont infinis, c’est, on peut le dire, l’opinion d’un homme qui n’est pas versé dans les choses qu’il faut savoir. p122
(voir les solides d'Archimède !)

Mais n’y en a-t-il qu’un ou y en a-t-il en réalité cinq ?

La question ainsi limitée, le doute est plus raisonnable.

Quant à nous, nous déclarons que, selon toute vraisemblance,
il n’y a qu’un seul monde, bien qu’on puisse, d’après d’autres considérations, être d’un autre avis.